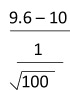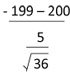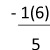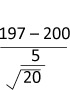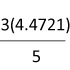|
|||||||||||||||||||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 9การทดสอบสมมติฐานค่าเฉลี่ยประชากรการทดสอบสมมติฐานค่าเฉลี่ยประชากรกลุ่มเดียว
เมื่อ μ คือค่าเฉล่ียของประชากรและ μ 0 คือค่าคงที่ที่ต้องการทดสอบ หรือเป็น
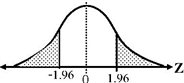
ค่าเฉลี่ยที่คาดว่าจะเป็น สมมติฐานที่จะทดสอบอยู่ในลักษณะ 1. H0 : μ = μ 0 แย้งกับ H1 : μ > μ 0 หรือ 2. H0 : μ = μ0 แย้งกับ H0 : μ < μ0 หรือ 3. H0 : μ = μ0 แย้งกับ H1 : μ ≠ μ0 ตัวสถิติที่ใช้ในการทดสอบขึ้นอยู่กับลักษณะของประชากรและขนาดตัวอย่างสุ่ม ซึ่ง แบ่งเป็น 3 กรณีคือ
ประชากรมีการแจกแจงแบบปกติและทราบค่าความแปรปรวน
ประชากรมีการแจกแจงแบบใด ๆ และไม่ทราบค่าความแปรปรวน
ประชากรมีการแจกแจงแบบใด ๆ และไม่ทราบค่าความแปรปรวน
Ex.1บริษัทผลิตอาหารสุนัขแห่งหนึ่งรับประกันว่าอาหารสุนัขที่ผลิตในแต่ละถุงจะมีน้ำหนักเฉลี่ย 10 กิโลกรัม
ส่วนเบี่ยงเบนมาตรฐาน 1 กิโลกรัม อาทิตย์เป็นพ่อค้ารายย่อยจำหน่ายอาหารสุนัขต้องการพิสูจน์ว่า การรับประกันของบริษัทแห่งนี้เป็นจริงหรือไม่ จึงสุ่มอาหารสุนัขมา
จำนวน 100 ถุง พบว่ามีน้ำหนักเฉลี่ย 9.6 กิโลกรัม ที่ระดับนัยสำคัญที่ 0.05 อาทิตย์จะสรุปการรับประกันของบริษัทเป็นจริงได้หรือไม่
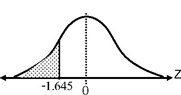
Ex.2น้ำตาลชนิดบรรจุขวดตราหนึ่ง พิมพ์ข็อความบนฉลากว่า “ นํ้าหนักสุทธิ 200 กรัม ” ผู้บริโภครายหนึ่ง สงสัยว่าข้อความดังกล่าวเกินความเป็นจริง จึงทำการสุ่มน้ำตาลตราดังกล่าวมา จำนวน 36 ขวด พบว่า นํ้าหนักสุทธิมีค่าเฉลี่ย 199 กรัม
และมีความแปรปรวนเท่ากับ 25 กรัม ที่ระดับนัยสำคัญ 0.05 ข้อสงสัยของผู้บริโภครายนี้เป็นความจริงหรือไม่
Ex.3กาแฟชนิดบรรจุซองยี่ห้อหนึ่ง พิมพ์ข้อความบนฉลากว่า “ นํ้าหนักสุทธิ 200 กรัม ” ผู้บริโภครายหนึ่ง สงสัยว่าข้อความดังกล่าวเกินความเป็นจริง
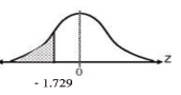
จึงทำการสุ่มมกาแฟตราดังกล่าวมา จำนวน 20 ซอง พบว่า นํ้าหนักสุทธิมีค่าเฉล่ีย 197 กรัม และมีความแปรปรวนเท่ากับ 25 กรัม ที่ระดับนัยสำคัญ 0.05 ข้อสงสัยของผู้บริโภครายนี้เป็นความจริงหรือไม่
พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย
|
| |||||||||||||||||||||||||
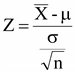
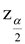 หรือ Z ≤
หรือ Z ≤ 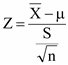
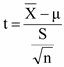 โดยมีค่า df = n - 1
โดยมีค่า df = n - 1 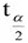 หรือ T ≤
หรือ T ≤ 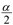 = 0.025
= 0.025