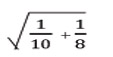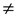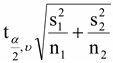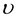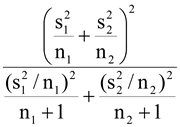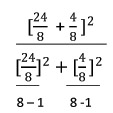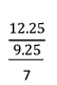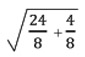|
|||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 6การประมาณค่าผลต่างค่าเฉลี่ยของสองประชากรการประมาณค่าเฉลี่ยผลต่างระหว่างค่าเฉลี่ยของประชากรสองชุด เป็นการศึกษาว่าปัจจัยเชิงคุณภาพมีผลทำให้ปัจจัยเชิงปริมาณของประชากร 2 กลุ่ม มีค่าแตกต่างกันประมาณเท่าใด กำหนดให้ 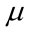 1 = ค่าเฉลี่ยของประชากรกลุ่มที่ 1 1 = ค่าเฉลี่ยของประชากรกลุ่มที่ 1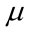 2 = ค่าเฉลี่ยของประชากรกลุ่มที่ 2 2 = ค่าเฉลี่ยของประชากรกลุ่มที่ 2
โดยมีการประมาณค่าผลต่างค่าเฉลี่ยของสองประชากรเป็น 2 วิธี คือ
การประมาณค่ามี 2 แบบ คือ 1. การประมาณค่าผลต่งค่าเฉลี่ยของสองประชากรแบบจุด (Point Estimation) 1 – 1 –  2 เป็นค่าประมาณแบบจุดของ 2 เป็นค่าประมาณแบบจุดของ
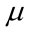 1 - 1 - 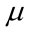 2 2  1 = ค่าเฉลี่ยของตัวอย่างกลุ่มที่ 1 1 = ค่าเฉลี่ยของตัวอย่างกลุ่มที่ 1 2= ค่าเฉลี่ยของตัวอย่างกลุ่มที่ 2 2= ค่าเฉลี่ยของตัวอย่างกลุ่มที่ 2
Ex.1จากการสอบถามอายุของประชากรในหมู่บ้านสองกลุ่ม
ให้
2. การประมาณค่าผลต่างค่าเฉลี่ยของสองประชากรแบบช่วง (Interval Estimation)1. เมื่อประชากรทั้งสองมีการแจกแจงแบบปกติและรู้ความแปรปรวนประชากร( 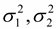 ) )ใช้ตัวสถิติ z ในการสร้างช่วงความเชื่อมั่น ให้  1 เป็นค่าเฉลี่ยของตัวอย่างขนาด n 1 ที่สุ่มมาจากประชากรที่ 1 ที่มีการ
แจกแจงแบบปกติและมีค่าความแปรปรวน 1 เป็นค่าเฉลี่ยของตัวอย่างขนาด n 1 ที่สุ่มมาจากประชากรที่ 1 ที่มีการ
แจกแจงแบบปกติและมีค่าความแปรปรวน  ให้  2 เป็นค่าเฉลี่ยของตัวอย่างขนาด n 2 ที่สุ่มมาจากประชากรที่ 2
ที่มีการแจกแจงแบบปกติและมีค่าความแปรปรวน 2 เป็นค่าเฉลี่ยของตัวอย่างขนาด n 2 ที่สุ่มมาจากประชากรที่ 2
ที่มีการแจกแจงแบบปกติและมีค่าความแปรปรวน 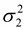 ดังนั้นช่วงความเชื่อมั่น ( 100 - 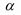 ) % ของผลต่างของค่าเฉลี่ยของสองประชากร ) % ของผลต่างของค่าเฉลี่ยของสองประชากร
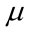 1 - 1 - 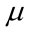 2 จากสูตร 2 จากสูตร 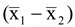 - - 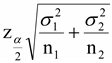 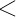 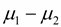 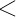
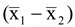 + + 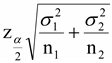
Ex.2 จากการสุ่มตัวอย่างการใช้วิทยุมือถือ สอง ชนิด คือ ชนิด A และ ชนิด B ชนิดละ 25 เครื่อง
พบว่ามีอายุการใช้งานเฉลี่ย 1,400 ชั่วโมง และ 1,200 ชั่วโมง ตามลำดับ ถ้าอายุการใช้งานของวิทยุมือถือทั้งสองชนิดมีการแจกแจงปกติ และมีส่วนเบี่ยงเบนมาตรฐาน
ของอายุการใช้งานเป็น 200 และ 100 ชั่วโมงตามลำดับ จงประมาณผลต่างอายุการใช้งานเฉลี่ยของวิทยุมือถือทั้งสอง ที่ระดับความเชื่อมั่น 95 %
2. เมื่อประชากรทั้งสองมีการแจกแจงแบบปกติแต่ไม่รู้ความแปรปรวนประชากร(
Ex.3 จากการสุ่มนักศึกษาวิทยาลัยอาชีวศึกษาสุโขทัย จำนวน 2 กลุ่ม ๆ ละ 30 คน ทำแบบทดสอบวิชาสถิติ
แบบเดียวกันได้คะแนนเฉลี่ย 67 และ 60 คะแนน ตามลำดับ และส่วนเบี่ยงเบนมาตรฐาน 5.8 และ 3.5 ตามลำดับ จงประมาณค่าตวามแตกต่างคะแนนเฉลี่ยของนักศึกษา
ทั้งสองกลุ่มที่ระดับความเชื่อมั่น 90 %
(67 - 60) - 1.645 .
3. เมื่อประชากรทั้งสองมีการแจกแจงแบบปกติแต่ไม่รู้ความแปรปรวนประชากร(
Ex.4 จากการสุ่มนักศึกษาวิทยาลัยอาชีวศึกษาสุโขทัย จำนวน 2 กลุ่ม กลุ่มที่ 1 จำนวน 10 คน และกลุ่มที่ 2 จำนวน 8 คน ทำแบบทดสอบวิชาสถิติ
แบบเดียวกันได้คะแนนเฉลี่ย 85 และ 60 คะแนน ตามลำดับ และส่วนเบี่ยงเบนมาตรฐาน 5 และ 7 ตามลำดับ ถ้าสมมติว่านักศึกษาทั้งสองกลุ่ม
ได้จากประชากรที่แจกแจงปกติ ซึ่งมีค่าความแปรปรวนเท่ากัน
จงประมาณค่าตวามแตกต่างคะแนนเฉลี่ยของนักศึกษา
ทั้งสองกลุ่มที่ระดับความเชื่อมั่น 99 %
3.2 เมื่อรู้ค่า
Ex.5 จากการสุ่มนักศึกษาวิทยาลัยอาชีวศึกษาสุโขทัย จำนวน 2 กลุ่ม กลุ่มที่ 1 จำนวน 8 คน และกลุ่มที่ 2 จำนวน 8 คน พบว่ามีค่าใช้จ่ายเฉลี่ยต่อวัน
เป็น 38 และ 34 บาท ตามลำดับ และค่าความแปรปรวนเป็น 24 และ 4 ตามลำดับ ถ้าสมมติว่านักศึกษาทั้งสองกลุ่ม
ได้จากประชากรที่แจกแจงปกติ ซึ่งมีค่าความแปรปรวนไม่เท่ากัน
จงประมาณค่าความแตกต่างของค่าใช้จ่ายเฉลี่ยของนักศึกษา
ทั้งสองกลุ่มที่ระดับความเชื่อมั่น 90 %
วิธีทำ |
||||
| พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย | |||||
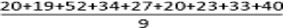
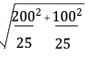
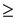 30 และ n2
30 และ n2 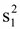 และ
และ 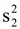
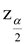
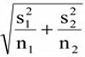
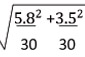
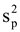 แทนความแปรปรวนตัวอย่าง
แทนความแปรปรวนตัวอย่าง
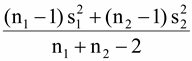
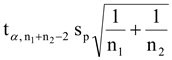
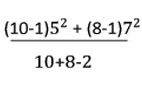
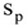 = 5.9582
= 5.9582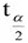 ,16
= 2.921
,16
= 2.921