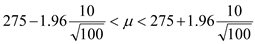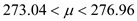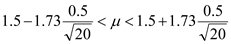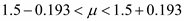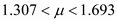|
||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 5การประมาณค่า (Estimation)การประมาณค่า เป็นวิธีการใช้ค่าสถิติที่ได้จากตัวอย่างไปประมาณค่าพารามิเตอร์ เป็นการหาข้อสรุปที่เกี่ยวกับพารามิเตอร์ ในลักษณะของการประมาณ ซึ่งมักแสดงในรูปตัวเลข เช่น ประมาณค่าเฉลี่ยของประชากร ประมาณค่าสัดส่วนของประชากร เป็นต้น อาจกล่าวได้ว่ากระบวนการในการประมาณค่า เป็นการนำตัวเลข ค่าสถิติที่ได้มาจากกลุ่มตัวอย่าง ไปประมาณหาค่าความจริงระดับประชากร ในเรื่องเดียวกันนั้น
การประมาณค่ามี 2 แบบ คือ 1. การประมาณค่าแบบจุด (Point Estimation)เป็นการประมาณค่าพารามิเตอร์ของประชากรด้วยค่าเพียงค่าเดียว (Single valued Estimation หรือ Point Estimation) ซึ่งการประมาณค่าแบบนี้อาจจะมีค่าเท่ากับค่าพารามิเตอร์หรืออาจมีโอกาสที่จะได้ค่าที่คาดเคลื่อนไปจากค่าพารามิเตอร์ได้มาก ทั้งนี้ขึ้นอยู่กับหน่วยตัวอย่างที่นำมาวิเคราะห์ (ถ้าหน่วยตัวอย่างนั้นได้มาจากการสุ่มตัวอย่าง ก็จะสามารถควบคุมความคลาดเคลื่อนได้ระดับหนึ่ง) หมายเหตุ การประมาณค่าพารามิเตอร์ซึ่งเป็นลักษณะของประชากรโดยใช้ข้อมูลตัวอย่าง หรือทำการประมาณค่าพารามิเตอร์ด้วยค่าสถิติ สัญลักษณ์ที่ใช้แทนค่าพารามิเตอร์และค่าสถิติ เช่น
ค่าที่ประมาณได้จากการประมาณค่าแบบจุด จะมีลักษณะเป็นตัวเลขประมาณค่าเดียว เรียกเป็น ค่าประมาณ (estimate) เช่น ประมาณค่าเฉลี่ยค่าใช้จ่ายในการรักษาพยาบาลของผู้ป่วยโรคหอบที่มารับการรักษาในโรงพยาบาลสุโขทัย เท่ากับ 4,950.-บาท
2. การประมาณค่าแบบช่วง (Interval Estimation)ค่าที่ประมาณได้จากการประมาณค่าแบบช่วง จะได้ช่วงของตัวเลขที่ประมาณ เรียก ช่วงการประมาณ เช่น ค่าเฉลี่ยค่าใช้จ่ายในการรักษาพยาบาลของผู้ป่วยโรคหอบที่มารับการรักษา ในโรงพยาบาลสุโขทัยอยู่ระหว่าง 3,370 - 6,480. บาท ในการประมาณค่าแบบช่วง นิยมเขียนเป็นสัญญลักษณ์ทางคณิตศาสตร์ แทนค่าที่ทำการประมาณโดยครอบคลุมค่าต่ำสุด - สูงสุด เช่น หากเป็นการประมาณค่าเฉลี่ยของประชากร คือ µ จะเขียนเป็น a < µ < b เรียกค่า a และ b ว่า ค่าต่ำสุด และค่าสูงสุดของช่วงประมาณ µ ในการประมาณค่าแบบช่วง นอกจาก ขึ้นอยู่กับค่าที่ต้องการประมาณ และการแจกแจงความน่าจะเป็นของค่าที่ต้องการประมาณแล้ว ยังขึ้นกับระดับความเชื่อมั่น (confidence level) อีกด้วย ระดับความเชื่อมั่นนี้ จะเป็นค่าที่บอกเราว่า ช่วงประมาณที่สร้างขึ้นจะครอบคลุมค่าพารามิเตอร์ด้วยความน่าจะเป็นมากน้อยเพียงใด ช่วงความเชื่อมั่น (confidence interval) หมายถึง ช่วงของค่าประมาณที่ประกอบไปด้วยค่าต่ำสุด (a) และค่าสูงสุด (b) ที่คำนวณขึ้นมา ช่วงดังกล่าวจะคลุมค่าของพารามิเตอร์ ด้วยความน่าจะเป็นตามที่กำหนด ตัวอย่างเช่น ช่วงความเชื่อมั่น 90% ของค่าใช้จ่ายโดยเฉลี่ยของผู้ป่วยโรคหอบที่มารับการรักษา ในโรงพยาบาลสุโขทัย อยู่ระหว่าง 3,370 - 6,480.-บาท หมายถึงว่า “มีความมั่นใจ 90% ที่ช่วงของการประมาณค่าใช้จ่ายโดยเฉลี่ยที่ได้ (3,370 - 6,480.-บาท) จะครอบคลุมค่าใช้จ่ายที่เป็นค่าเฉลี่ยจริงของผู้ป่วย” ที่ระดับบความเชื่อมั่นนี้ จะเขียนแทนด้วยสัญญลักษณ์ (1-α)100% โดยที่ 0 < α < 1 และเรียกค่า 1-α ว่า สัมประสิทธิ์ของความเชื่อมั่น (confidence coefficient) การประมาณค่าเฉลี่ยของประชากร
1.การประมาณค่าเฉลี่ยของประชากรกลุ่มเดียว
นั้นคือ
Ex.1จากการสอบถามอายุของนักเรียนกลุ่มหนึ่งเป็นดังนี้ 14 , 16 , 14 , 17 , 16 , 14 , 18 , 17
จงประมาณค่าเฉลี่ยเลขคณิตของอายุนักเรียนกลุ่มนี้ 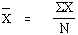 ประมาณค่าเฉลี่ย อายุนักเรียนกลุ่มนี้ 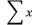 การประมาณค่าเฉลี่ยของประชากรกลุ่มเดียวแบบช่วง ค่าประมาณค่าเฉลี่ย 1 กลุ่มประชากรที่ระดับความเชื่อมั่น 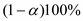 คือ คือ
1.กรณีทราบความแปรปรวนของประชากร
2.กรณีไม่ทราบความแปรปรวนของประชากร กลุ่มตัวอย่างขนาดใหญ่ (n
3.กรณีไม่ทราบความแปรปรวนของประชากร
กลุ่มตัวอย่างขนาดใหญ่ (n
เมื่อ
Ex.2
นักวิจัยผู้หนึ่ง ต้องการศึกษาระยะการตั้งครรภ์ของประชาชนในเขตอำเภอรอบนอกของจังหวัดสุโขทัย
จึงทำการสุ่มตัวอย่างมารดาที่มาฝากครรภ์และคลอดบุตรที่โรงพยาบาล จำนวน 100 ราย
พบว่ามีค่าเฉลี่ยระยะการตั้งครรภ์เป็น 275 วัน หากทราบว่าโดยทั่วไปทารกจะมีส่วนเบี่ยงเบนมาตรฐานของระยะการตั้งครรภ์เป็น 10 วัน
จงประมาณระยะการตั้งครรภ์เฉลี่ยของประชาชนนี้ (กำหนดระดับความเชื่อมั่น 95%)
แทนค่า n = 100
Ex.3
นักวิจัยผู้หนึ่งต้องการศึกษาถึงผลกระทบของการใช้ยาแอสไพรินของคนงานในโรงงาน กับการเป็นโรค
จึงได้ทำการสุ่มตัวอย่างคนงานในโรงงานแห่งหนึ่ง จำนวน 20 ราย ทำการวัดระดับ creatinine
พบว่ามีค่าเฉลี่ยเป็น 1.5 ความแปรปรวน 0.25 จงประมาณค่าเฉลี่ยระดับ creatinine ของคนงานในโรงงานนี้ (กำหนดระดับความเชื่อมั่น 90%)
แทนค่า n = 20 |
|||||||||
| พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย | ||||||||||

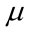
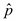
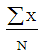 และ
และ 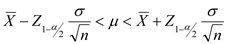
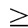 30)
30)
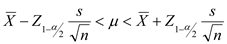
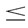 30)
30)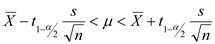 ซึ่งมีค่า df = n -1
ซึ่งมีค่า df = n -1 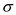 เป็นค่าส่วนเบี่ยงเบนมาตรฐานของประชากร
(และ
เป็นค่าส่วนเบี่ยงเบนมาตรฐานของประชากร
(และ 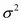 เป็นค่าความแปรปรวนของประชากร)
เป็นค่าความแปรปรวนของประชากร)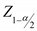 เป็นค่าสถิติ Z ที่เปิดได้จากตาราง (บางตารางใช้ค่า
เป็นค่าสถิติ Z ที่เปิดได้จากตาราง (บางตารางใช้ค่า 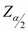 )
)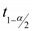 เป็นค่าสถิติ t ที่เปิดได้จากตาราง ที่ df=n-1
เป็นค่าสถิติ t ที่เปิดได้จากตาราง ที่ df=n-1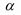 = .05 เปิดตารางค่า z ที่
= .05 เปิดตารางค่า z ที่ 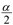 =.025 จะได้
=.025 จะได้