
|
|||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 4ค่ามาตรฐานหรือคะแนนมาตรฐาน (Standard Scores)ค่ามาตรฐานเป็นค่าที่บอกให้ทราบความแตกต่างระหว่างค่าของข้อมูลนั้นกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้นเป็นกี่เท่า ของส่วนเบี่ยงเบนมาตรฐาน สูตร Zi =  เมื่อ Zi คือ คะแนนมาตรฐาน XI คือ คะแนนดิบของข้อมูลที่มีค่าเฉลี่ยเลขคณิตที่จะแปลเป็นคะแนนมาตรฐาน  คือ ค่าเฉลี่ยเลขคณิต คือ ค่าเฉลี่ยเลขคณิตS.D. คือ ส่วนเบี่ยงเบนมาตรฐาน ในการเปรียบเทียบค่าคะแนนของข้อมูลที่มาจากข้อมูลต่างชุดกัน ว่าจะมีความแตกต่างกันอย่างไร ซึ่งบางครั้งไม่สามารถเปรียบเทียบได้โดยตรง เพราะค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของข้อมูลมักจะไม่เท่ากัน ในการเปรียบเทียบให้มีความถูกต้องจึงมีความจำเป็นต้องมีการเปลี่ยน คะแนนของข้อมูลทั้งสองชุดให้เป็นค่ามาตรฐาน( ซึ่งมีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐาน เท่ากันเสียก่อน ) จึงจะเปรียบเทียบข้อมูล 2 ชุดนี้ได้ ในการเปลี่ยนค่าของข้อมูลของตัวแแปรหรือข้อมูลแต่ละตัวให้เป็นค่ามาตรฐานที่นิยมใช้คือเปลี่ยนให้มีค่าเฉลียเลขคณิตเท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1
ข้อสังเกต
Ex1.
สมศักดิ์สอบวิชาสถิติและภาษาอังกฤษ ซึ่งมีคะแนนเต็ม 100 คะแนนเท่ากัน ในการสอบสายใจได้คะแนน 75 และ 85
คะแนนตามลำดับ ถ้าค่ามัชฌิมเลขคณิตและส่วนเเบี่ยงเบนมาาตรฐานของคะแนนสถิติของนักศึกษากลุ่มนี้คือ 60 และ 10 ค่าเลขคณิตและส่วนเฉลี่ยเบี่ยงเบนมาตรฐานของวิชาภาษาอังกฤษคือ 70 และ 12
ตามลำดับ แล้วจงเปรียบเทียบว่าสมศักดิ์เรียนวิชาไหนได้ดีกว่ากัน
Ex2.
ในการสอบวิชาบัญชีของนักศึกษาระดับปวส.ของวิทยาลัยอาชีวศึกษาสุโขทัย มีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานเป็น 64 และ 10 ตามลำดับ
ถ้าค่ามาตรฐานของคะแนนวิชาบัญชีของ นารีคือ 1.3 อยากทราบว่านารีสอบได้คะแนนเท่าไร
| ||||
| พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย | |||||
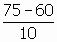 = 1.5
= 1.5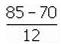 = 1.25
= 1.25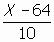
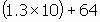 = 77
= 77