
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 2การวัดแนวโน้มเข้าสู่ส่วนกลาง (measures of central tendency)การวัดแนวโน้มเข้าสู่ส่วนกลางเป็นระเบียบวิธีทางสถิติในการหาค่าเพียงค่าเดียวที่จะใช้เป็นตัวแทนของข้อมูลทั้งชุด ค่าที่หาได้นี้จะทำให้สามารถทราบถึงลักษณะของข้อมูลทั้งหมดที่เก็บรวบรวมมาได้ ค่าที่หาได้นี้จะเป็นค่ากลาง ๆ เรียกว่า ค่ากลาง ประเภทของการวัดแนวโน้มเข้าสู่ส่วนกลาง การวัดแนวโน้มเข้าสู่ส่วนกลางมีอยู่หลายวิธีด้วยกัน ที่นิยมกันมาก ได้แก่ 1. มัชฌิมเลขคณิต (Arithmetic Mean) 2. มัธยฐาน (Median) 3. ฐานนิยม (Mode) ค่าเฉลี่ยเลขคณิต (Arithmetic Mean)1. ค่าเฉลียเลขคณิตของข้อมูลที่ไม่ได้แจกแจงความถี่ สามารถคำนวณได้จากสูตร  = = 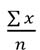 เมื่อ  (เอ็กซ์บาร์) คือ ค่าเฉลี่ยเลขคณิต (เอ็กซ์บาร์) คือ ค่าเฉลี่ยเลขคณิต คือ ผลบวกของข้อมูลทุกค่า คือ ผลบวกของข้อมูลทุกค่า คือ จำนวนข้อมูลทั้งหมด คือ จำนวนข้อมูลทั้งหมดEx.จากการสอบถามอายุของนักเรียนกลุ่มหนึ่งเป็นดังนี้ 14 , 16 , 14 , 17 , 16 , 14 , 18 , 17 จงหาค่าเฉลี่ยเลขคณิตของอายุนักเรียนกลุ่มนี้ วิธีทำ  = = 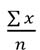  = = 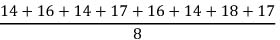 = =   = 15.75 = 15.75
ดังนั้นค่าเฉลี่ย อายุนักเรียนกลุ่มนี้ = 15.75 ปี 2. ค่าเฉลี่ยเลขคณิตของข้อมูลที่แจกแจงความถี่ สามารถคำนวณได้จากสูตร  = =  เมื่อ  (เอ็กซ์บาร์) คือ ค่าเฉลี่ยเลขคณิต (เอ็กซ์บาร์) คือ ค่าเฉลี่ยเลขคณิต คือ ความถี่ของข้อมูล คือ ความถี่ของข้อมูล 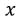 คือ ค่าของข้อมูล(ในกรณีการแจกแจงความถี่ไม่เป็นอันตรภาคชั้น) คือ ค่าของข้อมูล(ในกรณีการแจกแจงความถี่ไม่เป็นอันตรภาคชั้น) หรือ จุดกึ่งกลางของอันตรภาคชั้น(ในกรณีการแจกแจงความถี่เป็นอันตรภาคชั้น) หาได้จาก 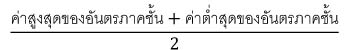  คือ ผลรวมความถี่ทั้งหมด หรือ จำนวนข้อมูลทั้งหมด คือ ผลรวมความถี่ทั้งหมด หรือ จำนวนข้อมูลทั้งหมด2.1 การหาค่าเฉลี่ยเลขคณิตข้อมูลที่แจกแจงความถี่ในกรณีที่ข้อมูลไม่เป็นอันตรภาคชั้น Ex.จากการสอบถามอายุของนักเรียนกลุ่มหนึ่งเป็นดังนี้ 14 , 16 , 14 , 17 , 16 , 14 , 18 , 17 จงหาค่าเฉลี่ยเลขคณิตของอายุนักเรียนกลุ่มนี้ วิธีทำ สร้างตารางแจกแจกความถี่ข้อมูล
 = =   = =   = 15.75 = 15.75 2.2 การหาค่าเฉลี่ยเลขคณิตข้อมูลที่แจกแจงความถี่ในกรณีที่ข้อมูลเป็นอันตรภาคชั้น (Class Interval) หรือเรียกสั้นๆ ว่า ชั้น หมายถึง ช่วงของคะแนนในแต่ละพวกที่แบ่ง Ex. จากข้อมูลในตารางแจกแจงความถี่ จงหาค่าเฉลี่ยเลขคณิต
วิธีทำ
 = =   = =   = 23.86 ปี = 23.86 ปี มัธยฐาน (Median)การหารค่ามัธยฐาน สามารถหาได้ 2 วิธี 1. การหามัธยฐานของข้อมูลที่ไม่แจกแจงความถี่ ซึ่งมีวิธีหาได้ดังนี้ 1.1 เรียงข้อมูลจากน้อิยไปมาก หรือจากมากไปน้อย 1.2 หาตำแหน่งของมัธยฐาน จาก 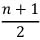 เมื่อ  = จำนวนข้อมูลทั้งหมด = จำนวนข้อมูลทั้งหมดEx. จงหามัธยฐานของข้อมูลต่อไปนี้ 9,10,5,11,14,6,16,17,13 วิธีทำ เรียงข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลที่มีค่ามากที่สุดคือ 5, 6, 9, 10, 11, 13, 14, 16,17 หาตำแหน่งมัธยฐาน 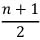 = =  = 5 = 5มัธยฐานของข้อมูล= 11 Ex.จงหามัธยฐานของข้อมูลต่อไปนี้ 40, 35, 24, 28, 26, 29, 36, 31, 42, 20, 23, 32 วิธีทำ เรียงข้อมูลจากข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลทีมีค่ามากที่สุดคือ 20, 23, 24, 26, 28, 29, 31, 32, 35, 36, 40, 42, ซึ่ง n = 12 ตำแหน่งมัธยฐาน = 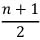 =  = 6.5 มัธยฐานอยู่ในตำแหน่ง ที่ 6.5 อยู่ระหว่าง 29 กับ 31 มัธยฐานเท่ากับ  มัธยฐานคือ 30 2. การหามัธยฐานของข้อมูลที่แจกแจงความถี่ คำนวณได้่จากสูตร 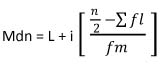
เมื่อ Mdn = มัธยฐาน ( Median ) L = ขีดจำกัดล่างที่แท้จริงของชั้นที่มีมัธยฐานอยู่ i = ความกว้างของอันตรภาคชั้น 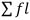 = ความถี่สะสมชั้นที่อยู่ก่อนชั้นที่มีมัธยฐานไปหาคะแนนน้อย = ความถี่สะสมชั้นที่อยู่ก่อนชั้นที่มีมัธยฐานไปหาคะแนนน้อย = ความถี่ของคะแนนในชั้นที่มีมัธยฐาน = ความถี่ของคะแนนในชั้นที่มีมัธยฐาน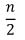 คือตำแหน่งมัธยฐาน คือตำแหน่งมัธยฐานEx. จากข้อมูลในตารางแจกแจงความถี่ จงหาค่ามัธยฐาน
วิธีทำ -หาความถี่สะสม
-หาตำแหน่งมัธยฐานจาก 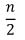 = =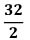 = 16
ค่ามัธยฐานที่อยู่ในชั้น 20 - 24
= 16
ค่ามัธยฐานที่อยู่ในชั้น 20 - 24
จากสูตร 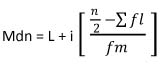
L = 20 - 0.5 = 19.5 i = 5 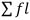 = 10 = 10 = 7 = 7แทนค่าในสูตร 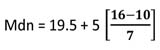 = 19.5 - 4.2
= 23.7 = 19.5 - 4.2
= 23.7มัธยฐานคือ 23.7 ฐานนิยม(Mode)การหารค่าฐานนิยม สามารถหาได้ 2 วิธี
1. ฐานนิยมของข้อมูลที่ไม่แจกแจงความถี่
Ex.จงหาฐานนิยมของข้อมูลต่อไปนี้ 3, 2, 4, 5, 6, 4, 8, 4, 7, 10
2. ฐานนิยมของข้อมูลที่แจกแจงความถี่
วิธีทำ . ค่าฐานนิยมอยู่ในอันตรภาคชั้น 20 -24 (ค่าที่มีความถี่มากที่สุด) จากสูตร  1. L = 20 - 0.5 = 19.5 2. i = 5 3. 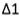 = 7 - 3 = 4 = 7 - 3 = 44. 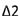 = 7 - 6 = 1 = 7 - 6 = 1แทนค่าในสูตร  = 19.5 + 4 = 23.5 = 19.5 + 4 = 23.5ดังนั้น ฐานนิยมของข้อมูลในตารางนี้คือ 23.5 ในกรณีที่หาค่ามัชฌิเลขคณิตและมัธยฐานได้แล้ว สามารถที่จะนำมาคำนวณหาฐานนิยมได้ โดยใช้สูตร Mode = 3Median - 2Mean |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 = 126
= 126