|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 13การวิเคราะห์สหสัมพันธ์ (Correlation Analysis)การวิเคราะห์สหสัมพันธ์ เป็นการศึกษาความสัมพันธ์ของตัวแปรตั้งแต่ 2 ตัวขึ้นไป ว่ามีความสัมพันธ์กันหรือไม่ สัมพันธ์กันมากน้อยเพียงใด โดยที่การวิเคราะห์สหสัมพันธ์จะแบ่งเป็น 2 ประเภท คือ 1. การวิเคราะห์สหสัมพันธ์อย่างง่าย (Simple Correlation Analysis) 2. การวิเคราะห์สหสัมพันธ์เชิงซ้อน (Multiple Correlation Analysis) ** ซึ่งในระดับนี้จะกล่าวเฉพาะการวิเคราะห์สหสัมพันธ์อย่าง่ายเท่านั้น ** การวิเคราะห์สหสัมพันธ์อย่างง่าย (Simple Correlation Analysis)ค่าสัมประสิทธิ์สหสัมพันธ์อย่างง่าย (Simple Correlation Coefficent) เป็นค่าที่วัดความสัมพันธ์ของ X กับ Y ว่า มีขนาดและทิศทางของความสัมพันธ์อย่างไร กำหนดให้ 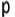 คือ สัมประสิทธิ์สหสัมพันธ์อย่างง่ายของประชากร
เมื่อ 1 คือ สัมประสิทธิ์สหสัมพันธ์อย่างง่ายของประชากร
เมื่อ 1 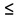 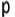 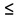 1
เนื่องจากในการวิเคราะห์สหสัมพันธ์ ไม่ได้เก็บข้อมูลจากประชากรแต่เป็นการเก็บข้อมูลจากกลุ่มตัวอย่าง
ดังนั้น ค่าสัมประสิทธิ์ที่ได้ จึงเป็นค่าสัมประสิทธิ์สหสัมพันธ์อย่างง่ายของตัวอย่าง โดยใช้สัญลักษณ์ ว่า r
เมื่อ 1 1
เนื่องจากในการวิเคราะห์สหสัมพันธ์ ไม่ได้เก็บข้อมูลจากประชากรแต่เป็นการเก็บข้อมูลจากกลุ่มตัวอย่าง
ดังนั้น ค่าสัมประสิทธิ์ที่ได้ จึงเป็นค่าสัมประสิทธิ์สหสัมพันธ์อย่างง่ายของตัวอย่าง โดยใช้สัญลักษณ์ ว่า r
เมื่อ 1 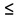 r r 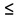 1 1สูตรในการคำนวณหาค่า r คือ r = 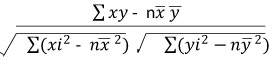 เมื่อ n = จำนวนตัวอย่าง  = ค่าเฉลี่ยของตัวแปร x = ค่าเฉลี่ยของตัวแปร x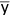 = ค่าเฉลี่ยของตัวแปร y = ค่าเฉลี่ยของตัวแปร yความหมายของค่า r 1. ค่า r เป็น + แสดงว่า x กับ y มีความสัมพันธ์ในทิศทางเดียวกัน 2. ค่า r เป็น แสดงว่า x กับ y มีความสัมพันธ์ในทิศทางตรงกันข้าม 3. ค่า r เป็น 0 แสดงว่า x กับ y ไม่มีความสัมพันธ์กันเลย 4. ค่า | r | มีค่าเข้าใกล้ 1 แสดงว่า x กับ y มีความสัมพันธ์กันมาก 5. ค่า | r | มีค่าเข้าใกล้ 0 แสดงว่า x กับ y มีความสัมพันธ์กันน้อย ค่าสัมประสิทธิ์การตัดสินใจ (Coefficent of Determination) เป็นค่าที่แสดงว่าตัวแปร x มีอิทธิพลต่อตัวแปร y มากน้อยเพียงใด โดยที่ค่าสัมประสิทธิ์การตัดสินใจ มีค่าเท่ากับ กำลังสองของสัมประสิทธิ์สหสัมพันธ์ หรือ 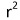 โดยที่ โดยที่ 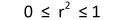
Ex.
แผนกวิจัยตลาดของบริษัททวีสิน จำกัด ต้องการศึกษาความสัมพันธ์ระหว่างยอดขายและค่าใช้จ่ายในการโฆษณา
โดยที่ข้อมูลเกี่ยวกับค่าใช้จ่ายและยอดขายในรอบ 8 ปีที่ผ่านมา มีดังนี้
จงคำนวณหาค่าสัมประสิทธิ์สหสัมพันธ์ (r) และสัมประสิทธิ์การตัดสินใจ (r2)
ของยอดขายสินค้าและค่าใช้จ่าย
พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
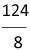 = 15.50
= 15.50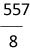 = 69.625
= 69.625