
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 12 การทดสอบไคสแคว์(Chi-Square Test: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ความคิด | เห็นด้วย | ไม่เห็นด้วย | ไม่มีความคิดเห็น |
| จำนวนผู้ตอบ | 12 | 12 | 24 |
จงทดสอบสมมุติฐานว่า ความคิดเห็นของครูวิทยาลัยอาชีวศึกษาสุโขทัยกระจายเป็นสัดส่วนที่เท่าๆกันที่ระดับ
นัยสำคัญ 0.05
วิธีทำ
1. ตั้งสมมติฐาน H0 = ความคิดเห็นของครูวิทยาลัยอาชีวศึกษาสุโขทัยกระจายเป็นสัดส่วนไม่แตกต่างกัน
H1 = ความคิดเห็นของครูวิทยาลัยอาชีวศึกษาสุโขทัยกระจายเป็นสัดส่วนที่แตกต่างกัน
2. สถิติที่ใช้ทดสอบ
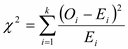 , pi =
, pi = 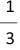
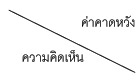 | Oi | Ei = npi | 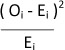 |
| เห็นด้วย | 12 | 16 | 1 |
| ไม่เห็นด้วย | 12 | 16 | 1 |
| ไม่มีความคิดเห็น | 24 | 16 | 4 |
| รวม | 48 | 48 | 6 |
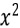 คำนวณ = 6
คำนวณ = 6
3. กำหนดระดับนัยสำคัญ 0.05
df = k - 1
df = 3 - 1 = 2
ดังนั้น 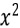 0.05,2 = 5.99
0.05,2 = 5.99
4. ค่าวิกฤต คือ 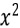 0.05,2 = 5.99
0.05,2 = 5.99
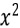 คำนวณ = 6 >
คำนวณ = 6 > 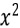 0.05,2 = 5.99
0.05,2 = 5.99
จึงปฎิเสธ H0
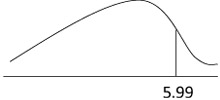
5. สรุปการทดสอบ นั่นคือ ความเห็นของครูวิทยาลัยอาชีวศึกษาเกี่ยวกับการขึ้นค่าระดมทรัพยากรแตกต่างกันอย่างมีนัยสำคัญที่ 0.05
การทดสอบสมมติฐานของข้อมูลกลุ่มตัวอย่างสองกลุ่ม(Two-way Classification )
การทดสอบในกรณีตัวแปรสองตัวนี้เป็นการทดสอบเพื่อดูว่า ตัวแปรสองตัวนี้มีความ เกี่ยวข้องหรือสัมพันธ์กันหรือไม่ ถ้าไม่สัมพันธ์กันหมายความว่าเป็นอิสระจากกันดังนั้นบางครั้งเรา จึงเรียกว่า การทดสอบความเป็นอิสระ (
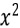 - test for independence) ข้อมูลที่ได้จะอยู่ใน
ระดับนามบัญญัติ (Norminal scale) ซึ่งอาจเป็นจำนวนความถี่ สัดส่วน ร้อยละ ก็ได้ โดยแต่ละ
ตัวแปรจะแบ่งเป็น 2 กลุ่ม หรือประเภทขึ้นไป เช่น เพศ (ชาย - หญิง) กับวุฒิการศึกษา (ป.ตรี
ป .โท ป.เอก) จะได้รูปแบบเป็น 2 x 3 ดังนั้นรูปแบบการวิเคราะห์อาจเป็นได้หลายรูปแบบขึ้นอยู่
กับจำนวนกลุ่มของแต่ละตัวแปร (2 x 2, 2 x 4, 3 x 2 เป็นต้น)
- test for independence) ข้อมูลที่ได้จะอยู่ใน
ระดับนามบัญญัติ (Norminal scale) ซึ่งอาจเป็นจำนวนความถี่ สัดส่วน ร้อยละ ก็ได้ โดยแต่ละ
ตัวแปรจะแบ่งเป็น 2 กลุ่ม หรือประเภทขึ้นไป เช่น เพศ (ชาย - หญิง) กับวุฒิการศึกษา (ป.ตรี
ป .โท ป.เอก) จะได้รูปแบบเป็น 2 x 3 ดังนั้นรูปแบบการวิเคราะห์อาจเป็นได้หลายรูปแบบขึ้นอยู่
กับจำนวนกลุ่มของแต่ละตัวแปร (2 x 2, 2 x 4, 3 x 2 เป็นต้น) การทดสอบโดยการใช้สูตร คำนวณ
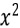 test คือ
test คือ
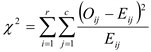
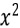 = ค่าสถิติไคสแควร์
= ค่าสถิติไคสแควร์
Oij = ความถี่ที่ได้จากการสังเกต (Observed Frequency) ในแถวที่ I คอลัมน์ที่ j
Ei = ความถี่ที่คาดหวัง (Expected Frequency ) ในแถวที่ I คอลัมน์ที่ j
ri = ผลรวมของแนวแนวนอน (Row)
cj = ผลรวมของแถวแนวตั้งหรือหลัก (Column)
n = ความถี่รวมทั้งหมด
และ Ei = 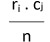
df = ( r - 1 ) ( c - 1 )
Ex.2ในการศึกษาความพึงพอใจของผู้ปกครองนักเรียนที่มีต่อการบริหารโรงเรียนโดย
เก็บข้อมูลกับผู้ปกครองอาชีพต่าง ๆ จำนวน 238 คน ได้ผลดังนี้
| อาชีพ | ระดับความพึงพอใจ | รวม | ||
| มาก | ปานกลาง | น้อย | ||
| ข้าราชการ | 30 | 20 | 7 | 57 |
| เกษตรกร | 40 | 30 | 12 | 82 |
| ค้าขาย | 47 | 33 | 19 | 99 |
| รวม | 117 | 83 | 38 | 238 |
จงทดสอบว่า อาชีพของผู้ปกครองเกี่ยวข้องกับความพึงพอใจในการบริหารโรงเรียนหรือไม่ ที่ระดับนัยสำคัญ 0.05
วิธีทำ
1. ตั้งสมมติฐาน H0 = อาชีพของผู้ปกครองไม่มีความเกี่ยวข้องกับความพึงพอใจ
H1 = อาชีพของผู้ปกครองความเกี่ยวข้องกับความพึงพอใจ
2. สถิติที่ใช้ทดสอบ
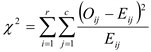
| Qij | Eij = 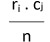 |
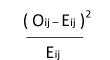 |
| 30 |  |
 |
| 20 | 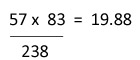 |
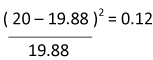 |
| 7 | 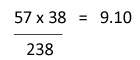 |
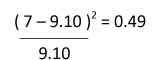 |
| 40 | 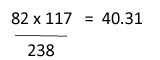 |
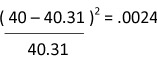 |
| 30 | 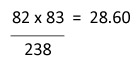 |
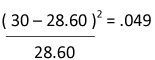 |
| 12 | 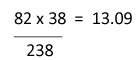 |
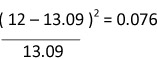 |
| 47 | 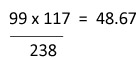 |
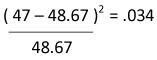 |
| 35 | 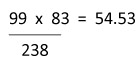 |
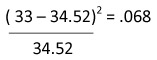 |
| 19 | 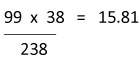 |
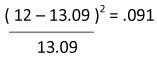 |
| 238 | 238 | 1.0704 |
df = ( r - 1 ) ( c - 1 )
df = 2.2 = 4 ดังนั้น
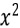 0.05,4 = 9.4848
0.05,4 = 9.4848 4. ค่าวิกฤต คือ
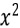 0.05,4 = 9.4848
0.05,4 = 9.4848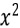 คำนวณ = 1.0704 <
คำนวณ = 1.0704 < 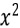 0.05,4 = 9.4848
0.05,4 = 9.4848จึงยอมรับ H0
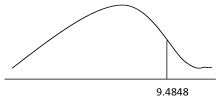
5. สรุปการทดสอบ นั่นคือ อาชีพของผู้ปกครองไม่มีความเกี่ยวข้องกับความพึงพอใจของการบริหารโรงเรียนที่ระดับนัยสำคัญ 0.05