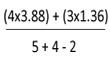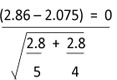|
|||||||||||||||||||||||||||
|
บทที่ 2 การวัดแนวโน้มเข้าสู่ส่วนกลาง บทที่ 3 การวัดการกระจาย บทที่ 4 ค่ามาตรฐาน บทที่ 5 การประมาณค่า บทที่ 6 การประมาณค่าผลต่างค่าเฉลี่ยสองประชากร บทที่ 7 การประมาณค่าสัดส่วน บทที่ 8 การทดสอบสมมติฐาน บทที่ 9 การทดสอบค่าเฉลี่ยประชากร บทที่ 10 การทดสอบผลต่างค่าเฉลี่ยสองประชากร บทที่ 11 การทดสอบสัดส่วนประชากร บทที่ 12 การทดสอบไคสแคว์ บทที่ 13 การเคราะห์สหสัมพันธ์ บทที่ 14 การวิเคราะห์การถดถอย |
บทที่ 10การทดสอบเกี่ยวกับผลต่างระหว่างค่าเฉลี่ยของสองประชากรเมื่อ μ1 - μ2 คือ ค่าผลต่างของคาเฉลี่ยของสองประชากรดังกล่าว
สมมติฐานท่ีจะทดสอบอยู่ในลักษณะ
ประชากรท้ังสองมีการแจกแจงแบบใด ๆ ไม่ทราบค่าความแปรปรวน σ12 และ σ22
ประชากรท้ังสองมีการแจกแจงแบบใด ๆ ไม่ทราบค่าความแปรปรวน σ12 และ σ22
2. เมื่อ σ 1 ≠ σ2
ให้ μ1 แทน คะแนนเฉลี่ยของนักศึกษาแผนกวิชาบัญชี
Ex.3
เภสัชกรต้องการต้องการทดสอบเซรุ่มใหม่ที่มีผลต่อการรักษาโรคลูคีเมียหรือไม่ โดยนำหนูที่เป็นโรคลูคีเมียขั้นรุนแรง จำนวน 9 ตัว โดยให้ 5 แรก ได้รับการฉีดเซรุ่ม
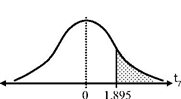
ปรากฎว่ามีอายุเฉลี่ยอยู่รอด 2.86 ปี ส่วนเบี่ยงเบนมาตรฐาน 1.97 ปี และหนูอีก 4 ตัวไม่ได้รับการฉีดเซรุ่ม มีอายุเฉลี่ยอยู่รอด 2.075 ปี ส่วนเบี่ยงเบนมาตรฐาน
1.17 ปี ถ้าเวลาของการอยู่รอดของหนูมีการแจกแจงปกติและมีความแปรปรวนเท่ากัน จงตรวจสอบดูว่าเซรุ่มมีผลต่อการรักษาโรคลูคีเมียที่ระดับ 0.05 หรือไม่
วิธีทำ
เมื่อความแปรปรวนสองประชากรเท่ากัน จะได้
พัฒนาโดยนายธีระพงษ์ กระการดี วิทยาลัยอาชีวศึกษาสุโขทัย
|
| |||||||||||||||||||||||||
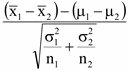
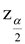 หรือ Z ≤
หรือ Z ≤ 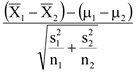
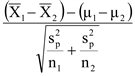
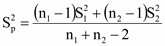
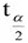 หรือ T ≤
หรือ T ≤ 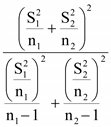
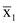 = 86.7
s1 = 6.28
= 86.7
s1 = 6.28
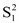 = 39.44
n1 = 50
= 39.44
n1 = 50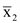 = 77.8
s2 = 5.61
= 77.8
s2 = 5.61
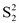 = 31.47
n2 = 50
= 31.47
n2 = 50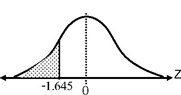

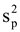 =
=